
Ongoing ResearchFaraday Rotation Measuresand the Structure of Astrophysical Plasmas |
|
.There are a number of ways one might probe the magnetic fields of astronomical objects. In dense, warm regions these include natural masers and the Zeeman splitting of atomic emission lines. However, for nearly completely ionized plasmas, such as that near black holes and in AGN jets, or cold plasmas, such as that in the interstellar medium, the only method available is the Faraday rotation of polarized background sources, induced by propagation through the magnetized plasma in the region of interest. First observed more than 150 years ago by Michael Faraday (you can see the original paper here!) after putting everything in his lab in his new, powerful magnet, Faraday rotation occurs due to the different phase velocities of the circularly polarized plasma eigenmodes. This is distinguishable from other polarization propagation effects due to its spectral dependence: the change in the polarization angle (Y) is proportional to the square of the wavelength (l) being observed. That is, Y = Y0 + RM l2 where Y0 is the intrinsic polarization angle of the source and RM is the “rotation measure” of the intervening plasma, linearly proportional to the cold electron density and projected magnetic field strength. Hence, by measuring the polarization angle at a number of wavelengths it is possible to determine the RM and therefore a density weighted average of the magnetic field strength. Recently, a number of authors have produce maps of the RM of AGN jets, noting the presence of nearly linear gradients in the RM across the jet in a number of cases. These are generally seen as evidence for a large-scale ordered helical magnetic field surrounding the jet. With Avi Loeb I have shown that helical motion in this surrounding material can leave dramatic imprints upon the observed RM’s, examples of which appear to match those profiles seen in 3C 273 remarkably well. With Jonathan McKinney, I have begun to generate the expected RM maps of self-consistent 3D jet simulations. The standard formula for the RM in a plasma with many field reversals depends critically upon the presence of strong mode coupling at the reversals themselves. In almost all cases this occurs. However, with Roger Blandford I have shown that at sufficiently low frequencies, it is possible to enter a regime in which the RM is no longer an average of the projected magnetic field but of the absolute value of the projected magnetic field. As a consequence, comparisons of high-frequency and low-frequency RM’s can potentially distinguish between large-scale and small-scale magnetic fields as well as identify the physical location of the rotating medium. |
|
Imaging BHs | The Nature of BHs | WD-CO Binaries | GRBs | Star Formation | Polarized RT | Magnetized NSs | Rotation Measures |
|
Papers on this topic: Broderick, A.E. & Blandford, R.D., 2010, ApJ (submitted) Broderick, A.E. & Loeb, A., 2009, ApJ, 703, 104L |
|
Home | Research | Publications | In the News | Pictures |




|
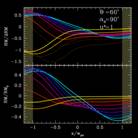
RM profiles across a rotating jet sheath with radial bulk Lorentz factor of 1.4, shown for a variety of velocity pitch angles (note that this is not the jet interior). There is a typical flattening associated with the toroidal jet motion. |
|
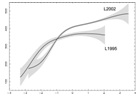
Actual RM profiles of knots in 3C 273 (Asada et al., 2008, ApJ, 675, 79). These show the flattening predicted above. |
|
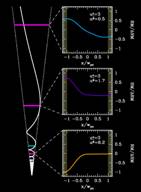
As the jet accelerates radial and expands, the velocity pitch angle decreases, resulting in a radial evolution of the RM profiles, seen here. |
|
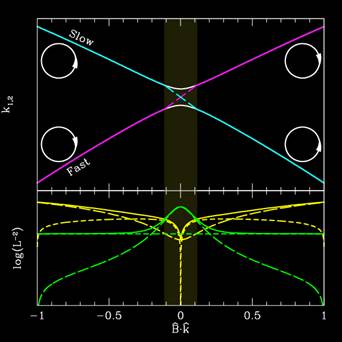
Propagation through magnetic field reversals differs qualitatively at high and low frequencies. In the former nearly perfect mode conversion maintains the polarization angle. In the latter adiabatic propagation results in a net reflection about an axis 45 degrees from the magnetic field. As a consequence, the observed RM changes sign at reversals. (Click to enlarge!) |
|
The frequency at which the character of the RM changes depends upon the length scale over which the magnetic field reverses and the plasma parameters at the reversals. With some assumptions we may use the high-frequency RM and the local magnetic field strength as proxies for these, identifying the transition frequency for a number of well-studied source classes. For nearby galactic nuclei this occurs above the ionospheric cut-off of roughly 10MHz. (Click to enlarge!) |