Ongoing Research

Strongly Magnetized Neutron Stars

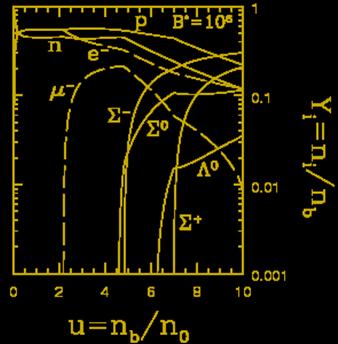
             Less massive than black holes and more massive than white dwarfs, neutron stars are some of the most compact configurations of matter known (as massive as the sun and 20 km across).  As a result, they are implicated in a number of high energy phenomena, ranging from pulsars to soft-gamma-ray repeaters to X-ray bursters and X-ray super-bursts.

             Due to their high density they are capable of supporting fields far stronger than possible in the laboratory.  Radio pulsars frequently have surface field strengths on the order of trillions of Gauss (the Earth’s field is approximately half a Gauss).  Magnetars can have fields up to a thousand times stronger!  The interior fields may be hundreds of times larger than those still.

             With Ramesh Narayan I’ve begun to study how the global structure of the interior magnetic field of a neutron star evolves.  Employing a variational energy principle we have found a number of quasi-stable states, similar to the well-known Spheromak states.  The violent relaxation of the interior magnetic configuration between these quasi-stable states can power the outbursts from soft-gamma-ray repeaters.

             In magnetars, the presence of the magnetic field can have a substantial effect upon the equation-of-state of neutron star matter.  There are two competing effects, Landau quantization (which tends to soften the equation-of-state), and baryon spin polarization (which tends to stiffen the equation-of-state).  With Madappa Prakash and Jim Lattimer, I have been involved in computing the equation-of-state within a relativistic mean-field theoretical framework.  In this we find that spin polarization dominates and leads to a net stiffening of the equation-of-state.

Imaging BHs | The Nature of BHs | WD-CO Binaries | GRBs | Star Formation | Polarized RT | Magnetized NSs | Rotation Measures

Papers on this topic:

          Broderick, A.E. & Narayan, R., 2007, MNRAS, 383, 943
Magnetic helicity and the relaxation of fossil fields

          Broderick, A.E., Prakash, M. & Lattimer, J.M., 2002, PhLB, 531, 167
Effects of strong magnetic fields in strange baryonic matter

          Broderick, A., Prakash, M. & Lattimer, J.M., 2000, ApJ, 537, 351
The Equation of State of Neutron Star Matter in Strong Magnetic Fields

Home | Research | Publications | In the News | Pictures

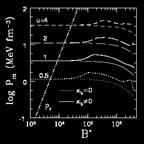
Pressure as a function of magnetic field (in units of electron critical fields) for various densities (in units of nuclear density) for a neutron-proton-electron-muon gas.

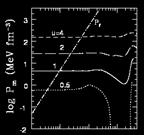
Same as above for interacting nuclear matter.

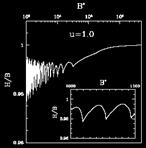
Ripples in the magnetization of nuclear matter due to the de Haas-van Alphen effect.

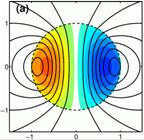
The poloidal (black lines) and toroidal (colored contours) of the minimum energy magnetic field configuration of a relaxed neutron star.  This is essentially a dipole!

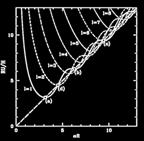
The energy per unit magnetic helicity (which is roughly conserved) as a function of the one free parameter in our solution for a number of field multipoles.  Each minimum is a quasi-stable state.

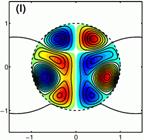
A complicated quasi-stable  state subject to a fixed surface field (e.g., a field frozen into the neutron star crust), chosen to roughly match a Kolmogorov spectrum.