White Dwarf-Compact Object Binaries

Home | Research | Publications | In the News | Pictures

Ongoing Research

White Dwarf—Compact Object Binaries

Papers on this topic:

Broderick, A.E. & Rathore, Y., 2006, MNRAS, 372, 923
A multidimensional, adiabatic hydrodynamics code for studying tidal excitation

Rathore, Y., Blandford, R. D. & Broderick, A.E., 2005, MNRAS, 357, 834
Resonant excitation of white dwarf oscillations in compact object binaries –I. The no back reaction approximation.

Rathore, Y., Broderick, A.E. & Blandford, R., 2003, MNRAS, 339, 25
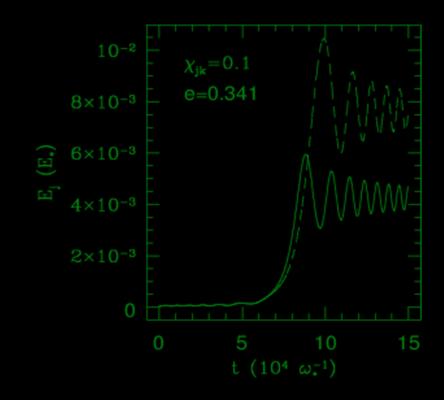
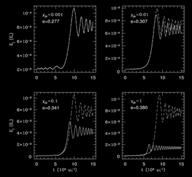
A variational formalism for tidal excitation: non-rotating, homentropic stars

White dwarfs are the most common endpoint of stellar evolution. As a result, white dwarf—compact object (either another white dwarf, a neutron star or a black hole) binaries seem to be unavoidable. As with other stellar (and planetary!) binaries the companions will exert tidal forces upon each other. Unique to white dwarfs though is their virtually nonexistent viscosity (once any crystallized core has been disrupted). As a result, tidally excited oscillations upon the white dwarf will not damp in the time it takes its orbit to shrink under the action of gravitational radiation. After passing through a succession of orbital resonances it is possible that enough energy can be transferred into the white dwarf to ignite a type Ia supernova! However, such an event would appear very different from standard type Ia supernovae since it will have occurred in the deep gravitational well of the compact companion.

With Yasser Rathore and Roger Blandford, I have been investigating the magnitude and direction of energy transfer in such a situation. With a linear perturbation analysis, we have found that indeed enough energy can be transferred to ignite the white dwarf, if it can be thermalized by non-linear processes. However, as oscillations on the white dwarf are excited energy is extracted from the orbit, which in turn back-reacts upon the excitation of the white dwarf. When this is important (roughly when the energy that can be extracted during the resonance is comparable to the orbital energy width of the resonance) it results in a diminished but uni-directional energy transfer.

Currently, we are trying to study the non-linear evolution of a large amplitude oscillation. For this purpose we have written an adiabatic, Eulerian, upwinded hydrodynamics code. We have been able to follow oscillations with amplitudes as small as 0.0001, and make direct comparisons with the linear perturbation theory. We are now investigating the energy cascade due to the non-linear mode-mode coupling.

The energy transfer during a passage through an orbital resonance with (solid) and without (dashed) back reaction for various ratios of the extracted energy to the energy width of the resonance.

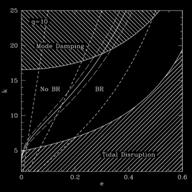
Regions in the resonance harmonic (related to the orbital semi-major axis) and eccentricity plane. For sufficiently high eccentricity the white dwarf is disrupted, and for sufficiently high resonances the modes can damp (via gravitational radiation!).

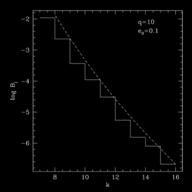
The energy of the fundamental quadrupolar mode as a function of resonance.